Question

Which is an exponential growth function?

f(x) = 6(0.25)x
f(x) = 0.25(5.25)x
f(x) = –4.25x
f(x) = (–1.25)x

Answer 1

The answer is f(x) = 0.25(5.25)x

Answer 2

Option 2

Explanation:

To find : Which is an exponential growth function?

Solution :

The exponential function general form is
`f(x)=ab^x`

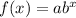
When b>1 then the function is exponentially grow.

When b<1 then the function is exponentially decay.

1)
`f(x)=6(0.25)^x`

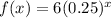
On comparing with general form, a=6 and b=0.25<1.

Function is not exponential growth function.

2)
`f(x)=0.25(5.25)^x`

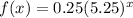
On comparing with general form, a=0.25 and b=5.25>1.

Function is an exponential growth function.

3)
`f(x)=(-4.25)^x`

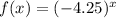
On comparing with general form, a=1 and b=-4.25<1.

Function is not exponential growth function.

4)
`f(x)=(-1.25)^x`

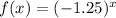
On comparing with general form, a=1 and b=-1.25<1.

Function is not exponential growth function.

Therefore, option 2 is correct.