Question

PLZ HELP ...The half-life of polonium-218 is 3.0 minutes. If you start with 40.0 g, how long will it be before only 4.5 g remains?

Answer 1

Answer:- 9.4 minutes.

Solution:- Radioactive decay obeys first order reaction kinetics and the equation used to solve this type of problems is:

`lnN=-kt+lnN_0`

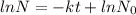
where, k is decay constant and t is the time.
`N_0` is the initial amount of the radioactive substance and N is the remaining amount.

Since the value of decay constant is not given, so we need to calculate it first from given half life by using the formula:

`k=(0.693)/(t_1_/_2)`

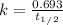
where
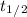`t_1_/_2` stands for half life.

Given half life is 3.0 minutes.

So,
`k=(0.693)/(3.0min)`

`k=0.231min^-^1`

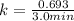
Let's plug in the values in the first order reaction equation and solve it for t.

`ln4.5g=-0.231min^-^1(t)+ln40.0g`

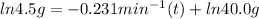
It could also be written as:

`ln((4.5g)/(40.0g))=-0.231min^-^1}`

`-2.18=-0.231min^-^1}`

`t=(-2.18)/(-0.231min^-^1)`

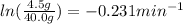
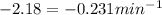
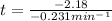
k = 9.4 min

So, the radioactive substance would take 9.4 minutes to decay from 40.0 grams to 4.5 grams.