SOLUTION - GIVEN = Two Points (0,-2,0) & (4, -3,0 ) which are inequidistant
from the all the points of plane.
Find out = Equation of plane
TO PROOF - The general equation of plane .
a ( x-x₀) + b ( y- y₀) + c(z-z₀) =0
let A = (0,-2,0) & B = (4, -3, 0 )
![\vec{AB}\vec{AB}= (4,-3,0)- ( 0,-2, 0)</p><p> = (4-0,-3+2,0-0)</p><p> = (4,-1,0)</p><p> ( All the points onthe plane are equidistant from A & B Then [tex]\vec{AB}]() is orthogonal to plane and become the normal vector.)
is orthogonal to plane and become the normal vector.)
let O be midpoint

O =
 ( 0+4, -2-3, 0-0 )
( 0+4, -2-3, 0-0 )
=\frac{1}{2} ( 4, -5, 0)
=

Equation of the plane by using the point & normal vector
by using general equation of a plane
4 ( x- 2) -1 (y +
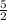 = 0
= 0
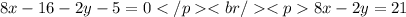
Hence Proved