Question

An architect designs a rectangular flower garden such that the width is exactly​ two-thirds of the length. If 310 feet of antique picket fencing are to be used to enclose the​ garden, find the dimensions of the garden.

Answer 1

The length and width of the garden are 93 feet and 62 feet respectively.

Step-by-step explanation

Suppose, the length of the rectangular garden is
`x` feet.

As the width is exactly​ two-thirds of the length, so the width of the garden will be:
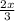`(2x)/(3)` feet.

310 feet of antique picket fencing are to be used to enclose the​ garden. It means, the perimeter of the garden is 310 feet.

Formula for perimeter of rectangle
`= 2(length+width)`

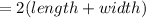
So, the equation will be....

`2(x+(2x)/(3))= 310\\ \\ x+(2x)/(3)= (310)/(2)\\ \\ (5x)/(3)=155\\ \\ 5x= 465\\ \\ x= (465)/(5)=93`

So, the length of the garden is 93 feet and the width is
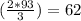`((2*93)/(3))=62` feet.