Answer:
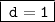
Explanation:
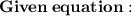

We need to find the value of d.

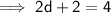
Step 1 :
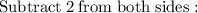
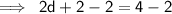
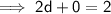
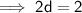
Step 2 :
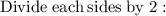
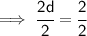
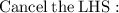
- Cancel 2 (which is on the numerator) and cancel 2 (which is on the denominator) by 2 :- [Leave d]
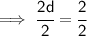


We know that 1d = d. So,
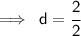
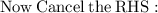
- Cancel 2 (which is on the numerator) and cancel 2(which is on the denominator) by 2 :
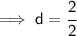
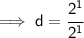

Hence, the value of d would be 1.

I hope this helps!
Let me know if you have any questions.