Answer : The correct option is, (B) 8.40 g
Solution : Given,
As we know that the radioactive decays follow the first order kinetics.
First, we have to calculate the half life of a potassium-40.
Formula used :
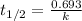
Now put the value of half-life, we get the value of rate constant.
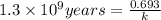
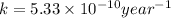
The expression for rate law for first order kinetics is given by :
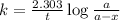
where,
k = rate constant =
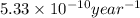
t = time taken for decay process =
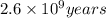
a = initial amount of potassium-40 = ?
a - x = amount left after decay process = 2.10 g
Now put all the values in above equation, we get
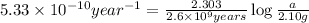
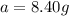
Therefore, the amount of potassium-40 in the sample originally was, 8.40 g