Question

A sample taken from a layer of mica in a canyon has 2.10 grams of potassium-40. A test reveals it to be 2.6 billion years old. How much potassium-40 was in the sample originally if the half-life of potassium-40 is 1.3 billion years? A. 4.20 g B. 8.40 g C. 12.6 g D. 16.8 g E. 25.2 g

Answer 1

Answer:The correct answer is option B.

Step-by-step explanation:

Initial amount of an isotope =
`N_o`

Final amount of an isotope = N

Half life of an isotope =
`t_{(1)/(2)}=1.3 \text{billion years}`

`\log N=\log N_o-(\lambda t)/(2.303)`

`\lambda =\frac{0.693}{t_{(1)/(2)}}=\frac{0.693}{1.3 \text{billion years}}=0.5330 (\text{billion years})^(-1)`

`\log[2.10 g]=\log N_o-\frac{0.5330 (\text{billion years})^(-1)* 2.6 \text{billion years}}{2.303}`

`0.9239=\log N_o`

`N_o=8.39266 g\approx 8.40 g`

Hence, the correct answer is option B.

Answer 2

Answer : The correct option is, (B) 8.40 g

Solution : Given,

As we know that the radioactive decays follow the first order kinetics.

First, we have to calculate the half life of a potassium-40.

Formula used :

`t_(1/2)=(0.693)/(k)`

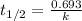
Now put the value of half-life, we get the value of rate constant.

`1.3* 10^9years=(0.693)/(k)`

`k=5.33* 10^(-10)year^(-1)`

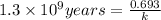
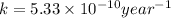
The expression for rate law for first order kinetics is given by :

`k=(2.303)/(t)\log(a)/(a-x)`

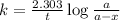
where,

k = rate constant =
`5.33* 10^(-10)year^(-1)`

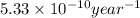
t = time taken for decay process =
`2.6* 10^9years`

a = initial amount of potassium-40 = ?

a - x = amount left after decay process = 2.10 g

Now put all the values in above equation, we get

`5.33* 10^(-10)year^(-1)=(2.303)/(2.6* 10^9years)\log(a)/(2.10g )`

`a=8.40g`

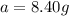
Therefore, the amount of potassium-40 in the sample originally was, 8.40 g