Question

I would like help with this physics problem

Answer 1

(a) This is a freefall problem in disguise - when the ball returns to its original position, it will be going at the same speed but in the opposite direction. So the ball's final velocity is the negative of its initial velocity.

Recall that

`v_f=v_i+at`

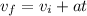
We have
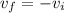`v_f=-v_i`, so that

`-2v_i=at\implies-2\left(8\,(\mathrm m)/(\mathrm s)\right)=\left(-2\,(\mathrm m)/(\mathrm s^2)\right)t\implies t=8\,\mathrm s`

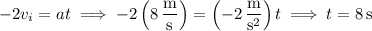
(b) The speed of the ball at the start and at the end of the roll are the same 8 m/s, so the average speed is also 8 m/s.

(c) The ball's average velocity is 0. Average velocity is given by
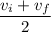`\frac{v_i+v_f}2`, and we know that
`v_f=-v_i`.

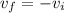(d) The position of the ball
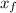`x_f` at time
`t` is given by

`x_f=x_i+v_it+\frac12at^2`

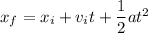
Take the starting position to be the origin,
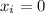`x_i=0`. Then after 6 seconds,

`x_f=\left(8\,(\mathrm m)/(\mathrm s)\right)(6\,\mathrm s)+\frac12\left(-2\,(\mathrm m)/(\mathrm s^2)\right)(6\,\mathrm s)^2=42\,\mathrm m`

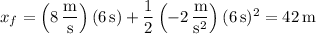
so the ball is 42 m away from where it started.

We're not asked to say in which direction it's moving at this point, but just out of curiosity we can determine that too:

`x_f-x_i=\frac{v_i+v_f}2t\implies42\,\mathrm m=\frac{8\,(\mathrm m)/(\mathrm s)+v_f}2(6\,\mathrm s)\implies v_f=6\,(\mathrm m)/(\mathrm s)`

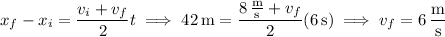
Since the velocity is positive, the ball is still moving up the incline.