Question

Solve this linear system using determinants: 2x + 3y = 6 −8x − 3y = 12 |A| = |Ax| =|Ay|=

Answer 1

in the photo provided.

Explanation:

Answer 2

The solution of the system is:
`x=-3` and
`y=4`

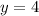
Explanation

Given linear system is ......

`2x+3y=6\\ \\ -8x-3y=12`

So, the co efficient matrix,
`A=\left[\begin{array}{cc}2&3\\-8&-3\end{array}\right]`

and the answer-column matrix :
`\left[\begin{array}{c}6\\12\end{array}\right]`

Now, we will replace the x and y column in the co efficient matrix by the answer-column matrix for getting
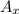`A_(x)` and
`A_(y)` respectively.

So,
`A_(x)= \left[\begin{array}{cc}6&3\\12&-3\end{array}\right]` and
`A_(y)= \left[\begin{array}{cc}2&6\\-8&12\end{array}\right]`

Now, we will find determinant of each matrix. So.....

`|A| = -6-(-24)= -6+24=18\\ \\ |A_(x)| =-18-36=-54\\ \\ |A_(y)|=24-(-48)=24+48=72`

According to the Cramer's rule,
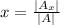`x= (|A_(x)|)/(|A|)` and
`y= (|A_(y)|)/(|A|)`

So....

`x= (-54)/(18)=-3\\ \\ y= (72)/(18)=4`