The length of that altitude is 5 cm.
Step-by-step explanation
According to the below diagram,
 is a parallelogram with diagonal
is a parallelogram with diagonal
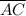 as its altitude.
as its altitude.
Suppose, the length of side
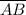 is
is
 cm.
cm.
As the length of one side is 1 cm longer than the length of the other, so the length of side
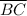 will be:
will be:
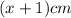
Given that, the perimeter of the parallelogram is 50 cm. So, the equation will be.....
![2[x+(x+1)]=50\\ \\ 2(2x+1)=50\\ \\ 4x+2=50\\ \\ 4x=48\\ \\ x= 12](https://img.qammunity.org/2019/formulas/mathematics/high-school/4vejrzo18l6zo5jn0pf5stjsu6injm157t.png)
So, the length of
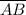 is 12 cm and the length of
is 12 cm and the length of
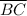 is (12+1)= 13 cm.
is (12+1)= 13 cm.
Suppose, the length of the altitude(
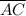 ) is
) is
 cm.
cm.
Now, in right angle triangle
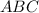 , using Pythagorean theorem....
, using Pythagorean theorem....
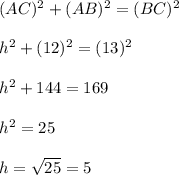
So, the length of that altitude is 5 cm.