Question

Your truck loan is $48,000 $48,000 with an APR of 6% 6% compounded annually for 7 7 years. The compound interest formula for this loan is A=$48,000(1.06 ) 7 . A=$48,000(1.06)7. If this loan was changed to be compounded monthly, what would the new annual percentage rate need to be for you to spend the same amount of money?

APR=8.8%
APR=5.8%
Apr=6.2%
APR=5.6%

Answer 1

i beilieve its apr=8.8%

Answer 2

Apr=6.2%

Explanation:

∵ Amount formula in compound interest,

`A=P(1+r)^t`

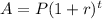
Where,

P = initial value,

r = rate per period,

t = number of periods,

Here, the given expression that represents the amount of loan after 7 years,

`A=4800(1.06)^7`

`=4800(1+0.06)^7`

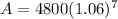
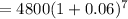
By comparing,

P = $ 4800, r = 0.06, t = 7 years,

If annual rate is 0.06, then, the rate per month = 0.06/12 = 0.005

Time = 7 × 12 = 84 months,

Hence, the amount would be,

`A=4800(1+0.005)^(84)`

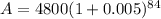
Let it is equivalent to the amount obtained in annual compound rate r for 7 years,

`\implies 4800(1+r)^7=4800(1+0.005)^(84)`

`(1+r)^7=(1.005)^(84)`

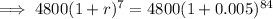
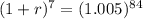
Taking log both sides,

`7\log (1+r) = 84 \log(1.005)`

`\log(1+r)=\log(1.005)`

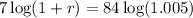
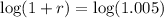
By graphing calculator,

r = 0.06168 ≈ 0.062 = 6.2 %