Question

The density of lead is 1.135×104 kg/m3.

What is the mass of a rectangular ingot of lead with dimensions 2.00 cm × 2.00 cm × 0.850 dm?

Answer 1

`\text{Density of lead =}1.135 * {10}^(4) \: \frac{kg}{ {m}^(3) }`

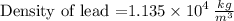
Dimension of rectangular ingot = 2.00 cm × 2.00 cm × 0.850 dm

1dm = 10cm
=> 0.850dm = 0.850×10 = 8.50 cm

Volume of ingot = 2.00 cm × 2.00 cm × 8.50 = 34.00 cm^3

1 m^3 = (100)^3 cm^3 = 10^6 cm^3

1 cm^3 = 1/10^6 = 10^(-6) m^3

34.00 cm^3 = 34 × 10^(-6) = 3.4 × 10^(-5) m^3

_____________-
Volume = 3.4×10^(-5) m^3

density = 1.135 × 10^4 kg/m^3

mass = density × volume =1.135 × 10^4 × 3.4×10^(-5) = 0.3859 kg
__________________

1kg = 1000g

0.3859 kg = 0.3859×1000 = 385.9 gram.

mass is 385.9 gram.

Answer 2

Mass = 385.9 g

Solution:

Data Given:

Density = 1.135 × 10⁴ Kg/m³ = 11.35 g/cm³

Volume = 2.0 cm × 2.0 cm × 0.850 dm

As (1 decimeter = 10 Centimeter) So,

Volume = 2.0 cm × 2.0 cm × 8.5 cm = 34 cm³

Formula Used:

Density = Mass ÷ Volume

Solving for Mass,

Mass = Density × Volume

Mass = 11.35 g/cm³ × 34 cm³

Mass = 385.9 g