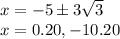Question

Can someone help me solve this please. I forgot how to so if you could explain please.

x^2 + 10x - 2 = 0

Answer 1

Hi,

Let's solve the equation step-by-step.

x2+10x−2=0

Step 1: Use quadratic formula with a=1, b=10, c=-2.

x= −b±√b2−4ac / 2a

x= −(10)±√(10)2−4(1)(−2) / 2(1)

x= −10±√108 / 2

x=−5+3√3 or x=−5−3√3

Answer:

x=−5+3√3 or x=−5−3√3

Have a great day!

Answer 2

So for this, I will be using the quadratic formula, which is
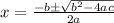`x=(-b\pm √(b^2-4ac))/(2a)` , with a = x^2 coefficient, b = x coefficient, and c = constant. Using our equation, plug the numbers in their appropriate spots:

`x=(-10\pm √(10^2-4*1*(-2)))/(2*1)`

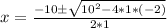
Next, solve the exponent and the multiplications:

`x=(-10\pm √(100-(-8)))/(2)\\\\x=(-10\pm √(100+8))/(2)`

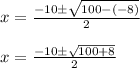
Next, solve the addition:

`x=(-10\pm √(108))/(2)`

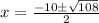
Next, apply the product rule of radicals here and simplify the radical:

• Product rule of radicals: √ab = √a × √b

`√(108)=√(6)* √(18)=√(3) * √(2) * √(9) * √(2) =3* 2* √(3)=6√(3)\\\\x=(-10\pm 6√(3))/(2)`

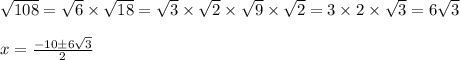
Next, divide:

`x=-5\pm 3√(3)}`

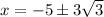
*The above is your exact solution. Approximates (rounded to the hundreths) are below:

Next, solve the equation twice, once with the + symbol and once with the - symbol:

`x=-5\pm 3√(3)}\\x=0.20, -10.20`