Answer: 153
Explanation:
When we have a group of N elements, the total number of combinations of K elements ( K ≤ N) is:

Where N! = N*(N - 1)*(N - 2)*...*2*1
In this case, we have a group of 18 people (then N = 18) and we want to see how many different combinations of 2 we can make (K = 2).
Using the above equation we get:
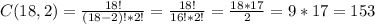
There are 153 different ways in which the manager can do this.