Question

A jar contains 4 red marbles numbered 1 to 4 and 10 blue marbles numbered 1 to 10. A marble is drawn at random from the jar. Find the probability the marble is blue or evennumbered.\

Answer 1

Explanation:

As per given , The jar contains

Red marbles = (R1) , (R2) , (R3) , (R4)

Blue marbles = (B1) , (B2) , (B3) , (B4) , (B5) , (B6) , (B7) , (B8) , (B9) , (B10) .

Total marbles = 4+10=14

The marbles that has even number = (R2) , (R4) ,(B2) , (B4) , (B6) , (B8) , (B10)

=7

Total Blue marbles = 10

Blue and even marbles = 5

Now , the number of marbles are blue or even numbered :

n(Blue or even )= n(Blue) + n(even)- n(Blue and even)

= 10+7-5 =12

Now , the probability the marble is blue or even numbered will be :

`P(\text{Blue or even }) = \frac{n(\text{Blue or even })}{\text{Total marbles}}\\\\=(12)/(14)=(6)/(7)`

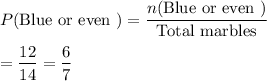
Hence, required probability =
`(6)/(7)`

Answer 2

we are given

A jar contains 4 red marbles numbered 1 to 4 and 10 blue marbles numbered 1 to 10

so, total number of marbles =10+4=14

the number of marble that is red or odd number=2

so, the probability of the marble is red or odd number is

`=(2)/(14)`

the probability the marble is blue or even numbered

= 1- P( the marble is red or odd number)

so, we get

the probability the marble is blue or even numbered is

`=1-(2)/(14)`

`=(12)/(14)`

`=(6)/(7)`...............Answer