A)
The Pythagorean theorem states that the sum of the squared legs is the squared hypothenuse:

If we divide the whole expression by
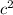 , we have
, we have
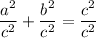
B)
The sine of x is the ratio between the opposite leg and the hypothenuse, while the cosine of x is the ratio between the adjacent leg and the hypothenues:
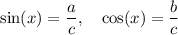
This means that
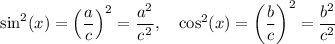
C)
From part B, we know that
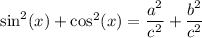
From part A, we know that this sum equals
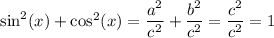
Which terminates the proof.