Given,
Perimeter of rectangle = 64 units.
Width = y = 11 units
Let,
Length = 20 units, as discussed in the question
Perimeter of rectangle = 2( length + width )
Solving Left Hand Side,
= > Perimeter of rectangle
= > 64 units [ Given ]
Solving Right Hand Side ,
= > 2( 20 + 11 )
= > 2( 31 )
= > 2 × 31
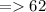
As we can see that 64 ≠ 62
64 ≠ 2( x + y )
Divide by 2 on both sides,
32 ≠ x + y
Hence, option B is correct.