Answer:- Energy =
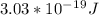 and frequency =
and frequency =
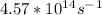 .
.
Solution:- The wavelength is given as 656.3 nm and it asks to calculate energy and frequency of a photon of this light. When the wavelength is given then the energy is calculated by using the equation:
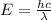
where, E is energy, h is planck's constant, c is speed of light and
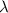 is the wavelength.
is the wavelength.
Wavelength is given in nm and for calculations of energy we need it in m.
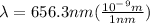
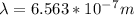
Let's plug in the values in the equation to calculate energy:
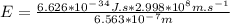
E =
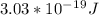
Frequency is calculated for the given wavelength using the equation:
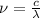
let's plug in the values in the equation:
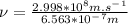

So, the energy of the photon for given wavelength is
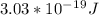 and the frequency is
and the frequency is
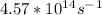 .
.