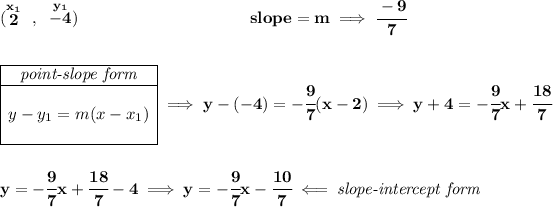parallel lines have the same exact slopes, thefore "q" must also have the same slope as "p", wait a second, what's p's slope anyway? let's see the equation, low and behold, the equation is already in point-slope form, therefore,

so we're really looking for the equation of a line whose slope is -9/7 and runs through (2, -4).