Answer:
6854640
Explanation:
Binomial expansion:
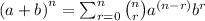
Term where power of second term is r.
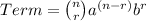
The given expression is
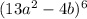
here, n=6.
We need to find the coefficient of the term
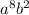 .
.
Power of b is 2, so the value of r is 2.
Using binomial expansion, we can find the term
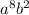 with its coefficient.
with its coefficient.
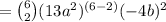

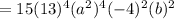
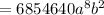
Therefore, the coefficient of the term
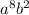 is 6854640.
is 6854640.