Answer:
A sequence of transformations that maps △RST to △R′S′T′ is a rotation of 90 degrees counterclockwise about the origin followed by a translation 1 unit up.
Explanation:
It is given that the coordinates of the vertices of △RST are R(−3, −1) , S(−1, −1) , and T(−4, −5).
The coordinates of the vertices of △R′S′T′ are R′(1, −2) , S′(1, 0) , and T′(5, −3).
If △RST rotated 90 degrees counterclockwise about the origin, then
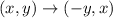
The vertices after rotation are

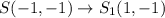
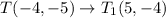
After that if the image translated 1 units up then
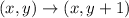
The vertices after rotation followed by translation are
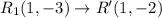

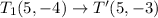
Therefore, a sequence of transformations that maps △RST to △R′S′T′ is a rotation of 90 degrees counterclockwise about the origin followed by a translation 1 unit up.