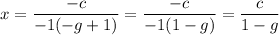Question

How do i solve g=(x-c)/x for x? I'm lost on problems like these with division problems and more than one x that I'm solving for.

Answer 1

The idea is to bring x to the numerators:

You start by saying
`x\\eq 0` (it's a denominator). Then you multiply both sides by x (which is legit, since you are multiplying for something which isn't zero). Then you get
`gx = x-c`. Add
`c-gx` to both sides, and you get - reading right to left -
`(1-g)x = c` and, AFTER stating that
`g \\eq 1` (you can't divide by zero!!)
`x= \frac {c}{1-g}`

Answer 2

you can group all the x together and then factor out x and then divide.

g = (x-c)/x

multiply both sides by x and u get

gx = x - c

move all x terms together... subtract x from both sides

gx - x = -c

factor out x via reverse distributive property

x(g-1) = -c

divide both sides by g-1

x = -c/(g-1)

if you want to make it look like the other answer (they are both equivalent), if you factor out a negative 1 from the denominator, you get

`x=(-c)/(-1(-g+1)) = (-c)/(-1(1-g)) = (c)/(1-g)`