Solution: We have to find the probability of randomly selecting four person committee consisting entirely of women from a pool of 12 men and 15 women.
The number of ways 4 women can be selected from 15 women is:
15C4

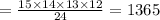
The number of ways 4 persons can be selected from total 12+15 = 27 persons is:
27C4
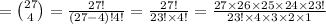
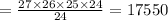
Therefore, the probability of randomly selecting four person committee consisting entirely of women from a pool of 12 men and 15 women is:

The event of selecting a woman and the event of selecting a woman the next time are dependent because the probability of selecting a woman at first draw is not same as the probability of selecting a woman at second draw.