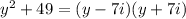Answer:
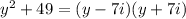
Explanation:
Given : Expression
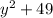
To find : Factor the expression over the complex numbers ?
Solution :
To factor the expression we equate it to zero and find the values of y,
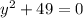
Subtract 49 both side,
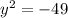
Taking root both side,
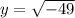
We know,
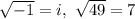
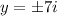
The factors are
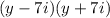
Therefore,