Question

the three sides of a triangle are n, 3n+2, and 4n−4. If the perimeter of the triangle is 54cm, what is the length of each side? Separate multiple entries with a comma.

Answer 1

The lengths of the sides are 7, 23 and 24.

In order to find this, we need to add all of the side lengths together and set equa to 54. This will allow us to solve for n.

n + 3n + 2 + 4n - 4 = 52

8n - 2 = 52

8n = 54

n = 7

This gives us the length of the first side. To solve for the others, plug 7 into the equations.

3n + 2

3(7) + 2

21 + 2

23

Then the next one.

4n - 4

4(7) - 4

28 - 4

24

Answer 2

Answer: 7cm , 23 cm and 24.

Explanation:

Given : The three sides of a triangle are n, 3n+2, and 4n−4.

We know that the perimeter of a polygon is the sum of all its sides.

Now, Perimeter of Triangle will be :-

`P=n+3n+2+4n-4=8n-2`

If the perimeter of the triangle is 54 cm , then we have

`8n-2=54`

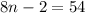
Add 2 both sides, we get

`8n=56`

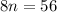
Divide both sides by 8, we get

`n=7`

Then , 3n+2 = 3(7)+2=23

4n-4 = 4(7)-4=24

Hence, the length of all its side will be 7cm , 23 cm and 24.