- Zero Product Property: if a × b = 0, then either a or b = 0 or both a and b = 0.
(Make sure to set f(x) to zero)
So for this equation, I will be factoring by grouping. Firstly, what two terms have a product of -5x^2 and a sum of 4x? That would be 5x and -x. Replace 4x with 5x - x:
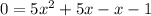
Next, factor 5x^2 + 5x and -x - 1 separately. Make sure that they have the same quantity on the inside:
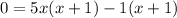
Now you can rewrite the equation as:
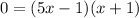
Now apply zero product property to the factors to solve for x:
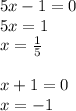
The x-intercepts are (1/5 ,0) and (-1,0).