Question

What are the x-intercepts of the graph of the quadratic function


`f(x) = 5x {}^(2) \ + 4x - 1`

Answer 1

• Zero Product Property: if a × b = 0, then either a or b = 0 or both a and b = 0.

(Make sure to set f(x) to zero)

So for this equation, I will be factoring by grouping. Firstly, what two terms have a product of -5x^2 and a sum of 4x? That would be 5x and -x. Replace 4x with 5x - x:
`0=5x^2+5x-x-1`

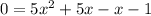
Next, factor 5x^2 + 5x and -x - 1 separately. Make sure that they have the same quantity on the inside:
`0=5x(x+1)-1(x+1)`

Now you can rewrite the equation as:
`0=(5x-1)(x+1)`

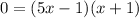
Now apply zero product property to the factors to solve for x:

`5x-1=0\\5x=1\\x=(1)/(5)\\\\x+1=0\\x=-1`

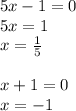
The x-intercepts are (1/5 ,0) and (-1,0).