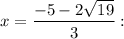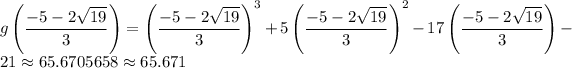Question

Help me please PRECAL

Answer 1

To find the local maximum of the function
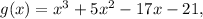`g(x)=x^3+5x^2-17x-21,` you should:

1. find the derivative
`g'(x)=3x^2+10x-17;`

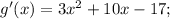
2. find stationary points. Equate derivative to zero and then solve the equation

`3x^2+10x-17=0,\\ \\D=10^2-4\cdot 3\cdot (-17)=100+204=304,\\ \\√(D)=4√(19) ,\\ \\x_(1,2)=(-10\pm 4√(19))/(2\cdot 3)=(-5\pm 2√(19))/(3).`

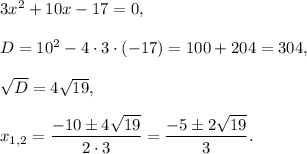
3. Determine signs of g'(x):

• when
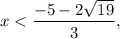  `x<(-5-2√(19))/(3),` then g'(x)>0 (function g(x) is increasing);
• when
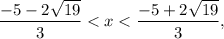  `(-5-2√(19))/(3)<x<(-5+2√(19))/(3),` then g'(x)<0 (function g(x) is decreasing);
• when
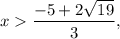  `x>(-5+2√(19))/(3),` then g'(x)>0 (function g(x) is increasing).

4. This means that
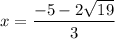`x=(-5-2√(19))/(3)` is point of maximum and
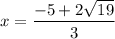`x=(-5+2√(19))/(3)` is point of minimum.

5. The maximum value of g(x) is at
`x=(-5-2√(19))/(3):`

`g\left((-5-2√(19))/(3)\right)=\left((-5-2√(19))/(3)\right)^3+5\left((-5-2√(19))/(3)\right)^2-17\left((-5-2√(19))/(3)\right)-21\approx 65.6705658\approx 65.671`