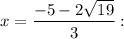To find the local maximum of the function
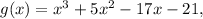 you should:
you should:
1. find the derivative
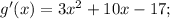
2. find stationary points. Equate derivative to zero and then solve the equation
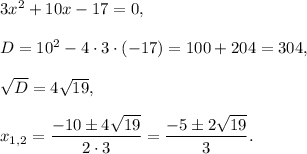
3. Determine signs of g'(x):
- when
 then g'(x)>0 (function g(x) is increasing);
then g'(x)>0 (function g(x) is increasing); - when
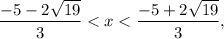 then g'(x)<0 (function g(x) is decreasing);
then g'(x)<0 (function g(x) is decreasing); - when
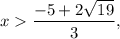 then g'(x)>0 (function g(x) is increasing).
then g'(x)>0 (function g(x) is increasing).
4. This means that
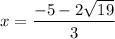 is point of maximum and
is point of maximum and
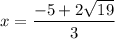 is point of minimum.
is point of minimum.
5. The maximum value of g(x) is at