Question

Determine whether the given point left parenthesis negative startfraction 1 over startroot 17 endroot endfraction comma startfraction 3 over startroot 17 endroot endfraction right parenthesis is on the unit circle

Answer 1

The given point does not lie on the unit circle.

Explanation:

We are given the following information in the question:

A unit circle is a circle with radius of 1 unit and has its center on the origin that is with coordinates (0,0).

Thus, the equation of unit circle is of the form:

`\text{Equation of circle}\\(x-h)^2 = (y-k)^2 + r^2\\\text{where (h,k) is the cenyer of the circle, r is the radius of the circle}\\\Rightarrow \text{Equation of unit cirle}\\(x-0)^2 + (y-0)^2 = (1)^2\\x^2 + y^2 = 1`

Now, we are given the point

`\bigg(\displaystyle(-1)/(√(17)),(3)/(√(17))}\bigg)`

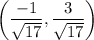
Putting this values in the equation of unit circle, we have:

`\bigg(\displaystyle(-1)/(√(17)),(3)/(√(17))}\bigg)\\\\x^2 + y^2 = 1\\\bigg(\displaystyle(-1)/(√(17))\bigg)^2 + \bigg((3)/(√(17))\bigg)^2 = (1)/(17) + (9)/(17) = (10)/(17) \\eq 1`

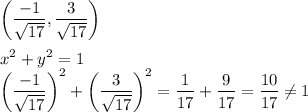
Thus, the given point does not lie on the unit circle.

Answer 2

It is not.

In order for the point to be on the unit circle, the sum of squares of the coordinates must be 1. You have (1² +3²)/17 = 10/17, not 1.

_____

The point (1/√17, 4/√17) would be on the unit circle.