We are given
The value -2 is a lower bound for the zeros of the function shown below f(x)=4x^3-12x^2-x+15
So, firstly, we will find value of f(x) at x=-2
we will plug x=-2 into f(x)
we get
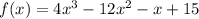
we will plug x=-2
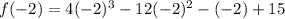
now, we can simplify it
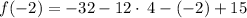
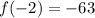
so,

we know that any zeros always lies between positive and negative value
Here , we got f(-3)=-63 ...which is negative value
so, this is lower bound
Hence , this is TRUE