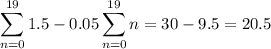Let's try to find a pattern to the sequence. You can see that we start from 1.5 and subtract 0.05 to generate the next element with each step. So, if we start from
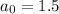 , the general formula for the n-th element is
, the general formula for the n-th element is
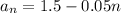
So, the sum of the first 20 terms is
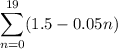
We can split the sum:
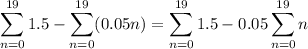
The first sum is independent of n, so we're just summing 1.5 for 20 times:

The second sum is 0.05 times the sum of the first 19 integers. The sum of the first k integers is given by
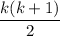
So, the sum of the first 19 integers is
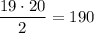
and 0.05 times this sum is
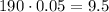
So, the sum of the first 20 elements of the sequence is given by