Consider the vertices of parallelogram JKLM with vertices J(2,2) , K(5,3) , L(5,-3) and M(2,-4).
Perimeter JKLM = Length JK + Length KL + Length LM + Length JM
Length JK = (2,2) (5,3)
The length(or distance) between two points say
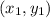 and
and
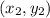 is given by the distance formula:
is given by the distance formula:
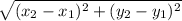
Now, length JK =
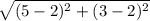
=
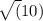 units
units
Since, JKLM is a parallelogram. In parallelogram opposite sides are equal in length.
Therefore, LM =
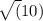 units
units
Now, length KL =
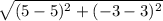
= 6 units
Since, JKLM is a parallelogram. In parallelogram opposite sides are equal in length.
Therefore, JM = 6 units
Perimeter of JKLM =
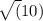 +
+
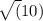 + 6 + 6
+ 6 + 6
= 2
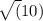 + 12
+ 12
= 18.324
Rounding to the nearest tenth, we get
= 18.3 units.
Therefore, the perimeter of JKLM is 18.3 units.