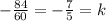Question

`(2)/(3) k - (k + (1)/(4)) = (1)/(12)k + (4)/(12) \\ \\`

Answer 1

use pemdas

Explanation:

Answer 2

Firstly, foil -(k + 1/4) (think of the minus sign as -1):

`(2)/(3)k-k-(1)/(4)=(1)/(12)k+(4)/(12)`

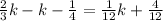
Next, combine like terms:

`-(1)/(3)k-(1)/(4)=(1)/(12)k+(4)/(12)`

Next, we have to add 1/3k on both sides, but first we have to find the LCD, or lowest common denominator, of 3 and 12. To do this, list the multiples of both and the lowest one they share is their LCD. In this case, the LCD is 12. Multiply both sides of -1/3 by 4/4 and 1/12 by 1/1:

`-(1)/(3)* (4)/(4)=-(4)/(12)\\\\(1)/(12)* (1)/(1)=(1)/(12)\\\\-(4)/(12)k-(1)/(4)=(1)/(12)k+(4)/(12)`

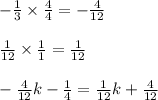
Now add 4/12k on both sides of the equation:

`-(1)/(4)=(5)/(12)k+(4)/(12)`

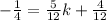
Next, to subtract 4/12 on both sides we need to find the LCD of 4 and 12. It's the similar process as we did with 12 and 3. This time the LCD is also 12. Multiply both sides of -1/4 by 3/3 and 4/12 by 1/1:

`-(1)/(4)* (3)/(3)=-(3)/(12)\\\\(4)/(12)* (1)/(1)=(4)/(12)\\\\-(3)/(12)=(5)/(12)k+(4)/(12)`

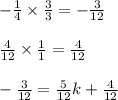
Now subtract 4/12 on both sides:

`-(7)/(12)=(5)/(12)k`

Lastly, multiply both sides by 12/5, and your answer will be:

`-(84)/(60)=-(7)/(5)=k`