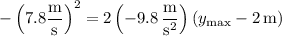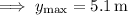Question

A basketball is shot from 2 meters up at an angle of 60° above the x axis at an initial velocity of 9 m/s. What is the maximum height the ball will reach?

Answer 1

I took the test and got 5.1 correct

Answer 2

The vertical component of the ball's initial velocity is

`v_(0y)=\left(9\,(\mathrm m)/(\mathrm s)\right)\sin60^\circ=7.8\,(\mathrm m)/(\mathrm s)`

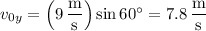
At any point along its trajectory, the vertical component of the ball's velocity
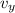`v_y` satisfies

`{v_y}^2-{v_(0y)}^2=2(-g)(y-2\,\mathrm m)`

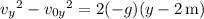
where
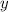`y` is the corresponding height of the ball while it's in the air. At its maximum height
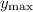`y_{\mathrm{max}}`, the ball's vertical velocity is 0, so we have

`-\left(7.8(\mathrm m)/(\mathrm s)\right)^2=2\left(-9.8\,(\mathrm m)/(\mathrm s^2)\right)(y_{\mathrm{max}}-2\,\mathrm m)`

`\implies y_{\mathrm{max}}=5.1\,\mathrm m`