Question

Factored form 20x^3+33x^2+7x

Answer 1

So firstly, the three terms share a GCF of x, so factor that out:
`x(20x^2+33x+7)`

Next, I'm going to be factoring by grouping. But first, what two terms have a product of 140x^2 and a sum of 33x? That would be 28x and 5x. Replace 33x with 5x + 28x:
`x(20x^2+5x+28x+7)`

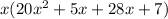
Now factor 20x^2 + 5x and 28x + 7 separately, make sure that they have the same quantity on the inside:
`x[5x(4x+1)+7(4x+1)]`

Now you can rewrite the expression as
`x[(5x+7)(4x+1)]` , which is your final answer.