Question

F the parent function f(x) = (2x − 3)3 is transformed to g(x) = (-2x + 3)3, which type of transformation occurs

Answer 1

The type of transformation is the reflection across the x-axis.

Explanation:

We are given a parent function f(x) by:

`f(x)=(2x-3)^3`

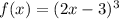
and the transformed function g(x) is given by:

`g(x)=(-2x+3)^3`

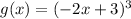
which could also be written as:

`g(x)=(-(2x-3))^3\\\\i.e.\\\\g(x)=(-1)^3\cdot (2x-3)^3\\\\i.e.\\\\g(x)=-(2x-3)^3\\\\i.e.\\\\g(x)=-f(x)`

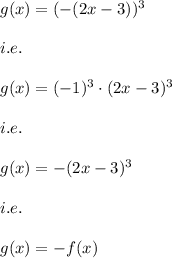
i.e. the transformation g(x) is obtained by reflecting the parent function f(x) across the x-axis.

( Since, when the reflection of a function is done across the x-axis then the x-coordinate of the point of the function remains the same and the y-coordinate of the point takes the negative sign.

i.e. f(x) → -f(x)

i.e.

(x,y) → (x,-y) )

Answer 2

f(x) = (2x - 3)³

g(x) = -(2x - 3)³ this is a reflection across the x-axis