Question

A customer borrowed $2000 and then a further $1000 both repayable in 12 months. What should he have saved if he had taken out one loan for $3000 repayable in 12 months?

Rates loans between $0- $2,500 are 10%

Rates loans between $2,501- $7,500 are 8%

a. $60

b. $240

c. $300

d. $360

e. $540

Answer 1

rate loan for 2000 is 10% so 200

rate loan for 1000 is 10% so 100

so together it's 300

rate loan for 3000 (out of one loan) is 8% so 240

So he would have saved 300-240 = 60 so a)

Answer 2

a. $60

Step-by-step explanation:

We will use simple interest formula to solve our given problem.

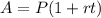`A=P(1+rt)`, where

A= Amount after t years.

P= Principal amount.

r= Interest rate in decimal form.

t= Time in years.

Let us find amount of loans repayable after 12 months for taking two amounts of $2000 and $1000.

As $2000 and $1000 are less than 2500, so the rate of loan will be 10%.

`10\%=(10)/(100)=0.10`

12 months = 1 year.

`A=2000(1+0.10* 1)`

`A=2000(1+0.10)`

`A=2000(1.10)`

`A=2200`

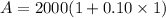
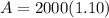
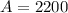
Now let us find amount repayable after 12 months for borrowing $1000.

`A=1000(1+0.10* 1)`

`A=1000(1+0.10)`

`A=1000(1.10)`

`A=1100`

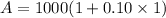
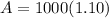
Adding these amounts we will get total repayable amount after 12 months for borrowing $2000 and $1000 separately.

`\text{Amount repayable for borrowing two separate amounts}=2200+1100=3300`

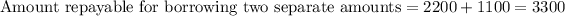
Now let us find repayable amount after 12 months for taking 1 loan. As $3000 is between $2501 and $7500, so rate of loan will be 8%.

`8\%=(8)/(100)=0.08`

`A=3000(1+0.08* 1)`

`A=3000(1+0.08)`

`A=3000(1.08)`

`A=3240`

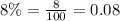
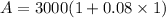
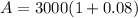
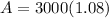
Now let us find difference between both repayable loan amounts.

`\text{Difference between both repayable loan amounts}=3300-3240`

`\text{Difference between both repayable loan amounts}=60`

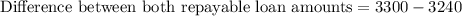
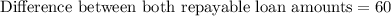
Therefore, the customer should have saved $60, if he had taken out one loan for $3000 and option a is the correct choice.