Hello!
To find the perimeter of the triangle, we need to find the length of all the sides using the distance formula.
The distance formula is:
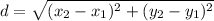 .
.
First, we can find the distance between the points (-3, -1) and (2, -1). The point (-3, -1) can be assigned to
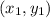 , and (2, -1) is assigned to
, and (2, -1) is assigned to
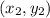 . Then, substitute the values into the formula.
. Then, substitute the values into the formula.
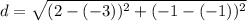
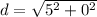

The distance between the points (-3, -1) and (2, -1) is 5 units.
Secondly, we need to find the distance between the points (2, 3) and (2, -1). Assign those points to
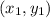 and
and
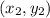 , then substitute it into the formula.
, then substitute it into the formula.

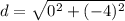
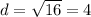
The distance between the two points (2, 3) and (2, -1) is 4 units.
Finally, we use the distance formula again to find the distance between the points (-3, -1) and (2, 3). Remember the assign the ordered pairs to
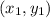 and
and
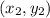 and substitute!
and substitute!
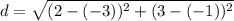
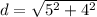
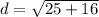
 This is equal to approximately 6.40 units.
This is equal to approximately 6.40 units.
The last step is to find the perimeter. To find the perimeter, add of the three sides of the triangle together.
P = 5 units + 4 units + 6.4 units
P = 15.4 units
Therefore, the perimeter of this triangle is choice A, 15.4.