Question

What are the values of the variables?

I am confused of what I need to do. I'm not sure if I find both x and y, or y or x.

Should I also equal both of these equations to find the answer?

Answer 1

I know that:

`2x+12+3x+23=180`

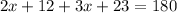
How do I know that? Well, according to the Alternate Interior Angles Theorem, I know that 2x+12 could also go right above 3x+23.

If that is the case, then they would both equal 180° because they would both sit on a straight line. Let's solve:

`5x+35=180`

`5x=145`

`x=29`

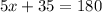
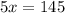
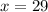
Now we know what x is equal to. Let's solve for y. I know that:

`2x+12+y=180`

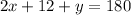
because they sit on a straight line. Since we have x, this is solvable. Let's plug in our x value and solve.

`2(29)+12+y=180`

`58+12+y=180`

`70+y=180`

`y=110`

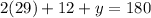
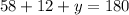
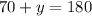
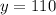
Your final answers would be:

`x=29`

`y=110`

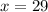
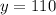
If you need to find the angles, just plug in these numbers for the variables and solve.