Question

What is the skew {1, 1, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 5, 5, 6, 8}

Answer 1

These are the steps to compute the skew:

• Compute the average of the dataset: sum all of the elements and divide by how many they are:

`(1+ 1+ 2+ 2+ 2+ 3+ 3+ 3+ 3+ 4+ 4+ 4+ 5+ 5+ 6+ 8)/(16) = 3.5`

• Compute the standard deviation: subtract the average from all elements, square the result, compute the average of this new dataset and take the square root of the result:

When you subtract the mean, you have

-2.5, -2.5, -1.5, -1.5, -1.5, -0.5, -0.5, -0.5, -0.5, 0.5, 0.5, 0.5, 1.5, 1.5, 2.5, 4.5

When you square the results, you have

6.25, 6.25, 2.25, 2.25, 2.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 2.25, 2.25, 6.25, 20.25

The average of this new dataset is

`\sigma^2 = 3.25`

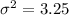
Whose square root, i.e. the standard deviation, is

`\sigma = √(3.25) = 1.8028`

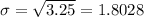
• Return to the dataset where you subtracted the mean from each point, and divide each point by the standard deviation:

-1.38675, -1.38675, -0.83205, -0.83205, -0.83205, -0.27735, -0.27735, -0.27735, -0.27735, 0.27735, 0.27735, 0.27735, 0.83205, 0.83205, 1.38675, 2.49615

• Cube these results:

-2.666828, -2.666828, -0.576035, -0.576035, -0.576035, -0.021335, -0.021335, -0.021335, -0.021335, 0.021335, 0.021335, 0.021335, 0.576035, 0.576035, 2.666828, 15.552940

• Sum all these numbers together: the result is 12.289.
• Divide this number by the total number of elements in the dataset:

`(12.289)/(16) = 0.76805`

And this is the skew.