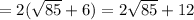Question

Find the perimeter of the parallelogram with these vertices. , 47 , , −31 , , 41 , , −3−5 give an exact answer (not a decimal approximation). simplify your answer as much as possible.

Answer 1

The perimeter of the parallelogram is
`2√(85)+12`

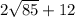
Step-by-step explanation

According to the diagram below, Vertices of the parallelogram ABCD are: A (-3, 1) , B (4, 7) , C (4, 1) and D (-3, -5)

Using distance formula.....

Length of AB
`= √((-3-4)^2+(1-7)^2)=√((-7)^2+(-6)^2)= √(49+36)=√(85)`

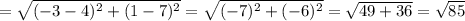
Length of BC
`=√((4-4)^2+(7-1)^2)=√(0+6^2)=√(36)=6`

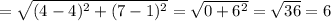
As the opposite sides are equal in any parallelogram, so
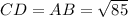`CD=AB=√(85)` and
`AD=BC= 6`

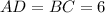
Thus the perimeter
`=2(√(85) +6)= 2√(85)+12`