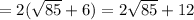The perimeter of the parallelogram is
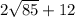
Step-by-step explanation
According to the diagram below, Vertices of the parallelogram ABCD are: A (-3, 1) , B (4, 7) , C (4, 1) and D (-3, -5)
Using distance formula.....
Length of AB
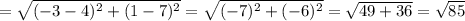
Length of BC
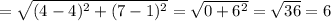
As the opposite sides are equal in any parallelogram, so
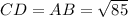 and
and
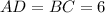
Thus the perimeter