Question

The probability that a flight departs on time is 0.83; the probability that it arrives on time is 0.82; and the probability that it departs and arrives on time is 0.78. find the probability that a plane arrives on time given that it departs on time, computed to the nearest two decimal points.

Answer 1

Solution: Let P(A) denotes the probability that the plane arrives on time and let P(D) denotes the probability that the plane departs on time. Therefore, we have:

`P(A) = 0.82, P(D)=0.83, P(A \cap D)=0.78`

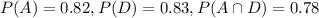
Now the probability that a plane arrives on time given that it departs on time is:

`P(A|D) = (P(A \cap D))/(P(D))`

`=(0.78)/(0.83) =0.94`

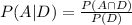
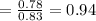
Therefore, the probability that a plane arrives on time given that it departs on time = 0.94