Answer:
The correct option is 2.
Explanation:
The given inequality is
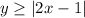
If a point is part of the solution of the inequality, then the inequality must be satisfied by that point.
Check the inequality for (0,0),
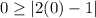
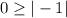
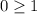
This statement is false. So (0,0) is not a solution.
Check the inequality for (1,1),
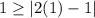
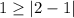
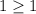
This statement is true. So (1,1) is a solution.
Check the inequality for (1,0),
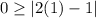
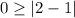
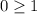
This statement is false. So (1,0) is not a solution.
Check the inequality for (3,2),
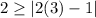

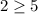
This statement is false. So (3,2) is not a solution.
Therefore the correct option is 2.