Let f(t) be the percentage of underage cigarette smokers t years after 1998.
We are also given that percentage of underage cigarette smokers was 49% (highest) in year 1998.
(A) We are supposed to assume (0,49) as vertex of our model.
Let us assume that our quadratic model is:
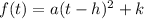
Upon substituting the vertex (h,k) = (0,49), we get:
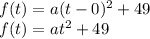
We can find the value of 'a' using the fact that in year 2006 (t = 8) there were 36% underage smokers.
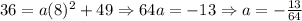
Therefore, the required quadratic model is

(B) In order to predict the percentage of underage smokers in year 2010, we will substitute t=12 in our quadratic model.
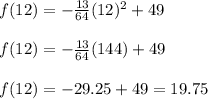
Therefore, there were 19.75% underage smokers in year 2010.