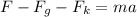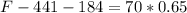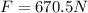Question

A box with a mass of 70 kg sits on a slope of 40 degrees. you are tasked with pushing the box up the slope. the static (stationary) coefficient of friction between the box and the slope is 0.55, and the kinematic (while moving) coefficient of friction is 0.35.

a. what is the minimum force required to keep the box from slipping?
b. what is the minimum force required to begin pushing the box up the slope?
c. what is the minimum force required to maintain the box moving up the slope?
d. what is the force required to accelerate the box up the slope at 0.65 m/s2 once it is already moving upwards? give your answers in newtons (n).

Answer 1

PART a)

Force of friction on the box is given by formula

`F_f = \mu mg cos\theta`

`F_f = 0.55 * 70 * 9.8 * cos40`

`F_f = 289 N`

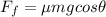
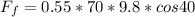
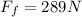
now the component of weight along the inclined

`F_g = mgsin40`

`F_g = 70*9.8 * sin40`

`F_g = 441 N`

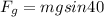
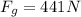
now by force balance the force required to hold the block

`F_(net) = F_g - F_f`

`F_(net) = 441 - 289 = 152 N`

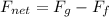
Part b)

to slide the block upwards the friction force will be upwards along the plane

`F = F_g + F_f`

`F = 441 + 289 = 730 N`

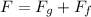
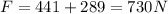
Part c)

Kinetic friction on the block is given by

`F_k = \mu_k mg cos\theta`

`F_k = 0.35 * 70 * 9.8 * cos40`

`F_k = 184 N`

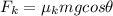
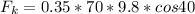
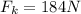
now in order to move it up

`F = F_g + F_k`

`F = 441 + 184`

`F = 625 N`

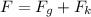
Part d)

now to accelerate upwards by 0.65 m/s^2 we can use

`F - F_g - F_k = ma`

`F - 441 - 184 = 70* 0.65`

`F = 670.5 N`