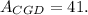1. Consider square ABCD. You know that
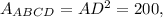
then
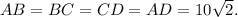
2. Consider traiangle AED. F is mipoint of AE and G is midpoint of DE, then FG is midline of triangle AED. This means that
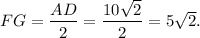
3. Consider trapezoid BFGC. Its area is
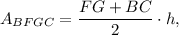 where h is the height of trapezoid and is equal to half of AB. Thus,
where h is the height of trapezoid and is equal to half of AB. Thus,
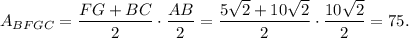
4.
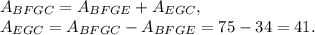
5. Note that angles EGC and CGD are supplementary and
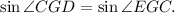
Then
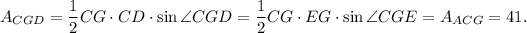
Answer: