Question

Lead metal can be extracted from a mineral called galena, which contains 86.6% lead by mass. a particular ore contains 68.5% galena by mass. part a if the lead can be extracted with 92.5% efficiency, what mass of ore is required to make a lead sphere with a 8.00 cm radius?

Answer 1

44kg

Step-by-step explanation:

Volume of the lead sphere is
`= 4/3*π*(r)3`

= 4/3*π*(8.0)3

= 4/3 * π * ( 512)

= 4/3 * 22/7 * (512)

= 2145.52 cm3

The consists of 68.5% galena while galena consists 86.6% lead.

Only 92.5% of the lead can be extracted.

Assuming X as the amount of ore needed

mass of ore can be determined as:

92.5% of 86.6% of 68.5% of X = 2145.52

0.925 * 0.866 * 0.685*X=2145.52

X=0.54871925/2145.52

`=44kg`]

Answer 2

The volume of sphere can be calculated using the following formula:

`V=(4)/(3)\pi r^(3)`

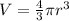
Here, r is radius of the sphere which is 8 cm. Putting the value,

`V=(4)/(3)\pi r^(3)=(4)/(3)(3.14)(8 cm)^(3)=2143.57 cm^(3)`

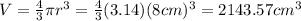
This is equal to the volume of lead, density of lead is
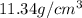`11.34 g/cm^(3)` thus, mass of lead can be calculated as follows:

`m=d* V=11.34 g/cm^(3)* 2143.57 cm^(3)=2.43* 10^(4)g`

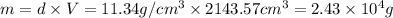
Let the mass of ore be 1 g, 68.5% of galena is obtained by mass, thus, mass of galena obtained will be 0.685 g.

Now, 86.6% of lead is obtained from this gram of galena, thus, mass of lead will be:

m=0.685×0.866=0.5932 g

Therefore, 0.5932 g of lead is obtained from 1 g of ore, if the efficiency is 100%.

For 92.5% efficiency, mass of lead obtained will be:

`m=(92.5)/(100)* 0.5932=0.5487 g`

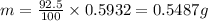
Thus, 1 g of lead obtain from
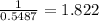`(1)/(0.5487)=1.822` grams of ore.

Thus,
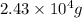`2.43* 10^(4) g` of lead obtain from:

`2.43* 10^(4)* 1.822=4.42* 10^(4)g=44.2 kg`

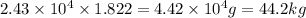
Therefore, mass of ore required to make lead sphere is 44.2 kg.