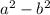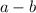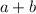Question

The volume (in cubic meters), vvv, of a rectangular prism is given by the expression: v = a^4-2a^2b^2+b^4v=a 4 −2a 2 b 2 +b 4 v, equals, a, start superscript, 4, end superscript, minus, 2, a, start superscript, 2, end superscript, b, start superscript, 2, end superscript, plus, b, start superscript, 4, end superscript where aaa and bbb are positive integers and a>ba>ba, is greater than,

b. pick three expressions that can represent the three unique dimensions of the prism (each in meters). choose all answers that apply: choose all answers that apply:

Answer 1

`{a}^(2) - {b}^(2)`

`a - b`

`a + b`

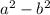
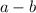
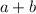
Explanation:

The given expression that represents the volume of the rectangular prism is:

`v = {a}^(4) - 2 {a}^(2) {b}^(2) + {b}^(4)`

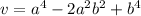
We can rewrite this to reveal a perfect square pattern.

`v =( { {a}^(2)) }^(2) - 2 {a}^(2) {b}^(2) + ( {b}^(2))^(2)`

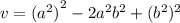
We factor using perfect squares to obtain:

`v = ( {a}^(2) - {b}^(2) )^(2)`

`v = ( {a}^(2) - {b}^(2) )( {a}^(2) - {b}^(2) )`

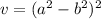
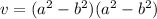
Volume is three dimensional so we need a third factor different from 1.

We further factor one of the difference of two squares to get:

`v = ( {a}^(2) - {b}^(2))(a - b)(a + b)`

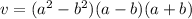
So pick the following unique dimensions from the possible answers:

`{a}^(2) - {b}^(2)`

`a - b`

`a + b`